만약 어떤 뉴런의 input x값과 output y 값을 알고 잇을때 어떤 W(가중치) 와 b(바이어스)를 넣어야지 원하는 y값에 도달하게 할수잇을까? w와 b에 임의값을 주어 원하는값을 찾는다는것은 거의 불가능 하다. 이때 필요한것이 backpropagation(역전파)라고 한다.
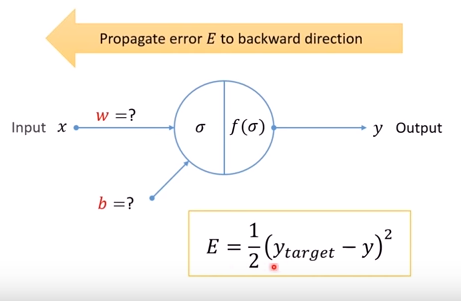
E는 오류 함수라고 하는데 구하자고 하는 값을 Y target 이라 하고 현재 Y의 차이의 제곱을 2로 나눈값으로 정의 하고있다.

E 와 W의 관계에 대한 그래프이다. 오류가 가장 적어지게 하는 W값이 어느 구간에 존재할텐데 그 구간을 미분을 통해서 알수가 있다. 오류가 작아지는 방향으로 W를 갱신 하다보면 원하는 값에 도달할수 있다. 이때 알파 값은 접근하는 속도인데 그 값이 너무 크다면 오류값의 계산에 오류가 생길 것이고 너무 작다면 W값을 찾는데 너무 많은 시간이 걸릴 것이다. 이두개의 가장 적절한 값을 배치 하는것이 중요하다. 지금 그래프에서는 미분값이 양수 이므로 반대 방향으로 가야하기 때문에 현재 가중치에 - 를 하는것이다.
(그래프가 이차 곡선을 이루므로 양수일때는 기울기가 0인 방향에 오른쪽에 있기 때문이다.)

이값은 어떻게 구할까??

가중치는 시그마에 영향을 미치고 시그마는 함수에 함수는 y(출력값)에 y는 오류 값에 영향을 미친다.
당연히 체인룰을 통해서 간단하게 구할수가 있다.
b(bias)값도 이와 같은 형식으로 우리는 구할수가 있다.
이제는 C++로 구현해보도록 하겠다.
class Neuron
{
public:
double w_;
double b_;
double input_;
double output_; // saved for back-prop
Neuron();
Neuron(const double& w_input,const double& b_input);
double getAct(const double& x);
double feedForward(const double& _input);
double getActGrad(const double& x);
void propBacward(const double& target);
};뉴런의 클래스 구조이다. 클래스 내의 각각의 함수를 살펴보자!(생성함수 제외)
double Neuron::feedForward(const double& _input) // 시그마와 함수 과정
{
input_ = _input;
const double sigma = w_ * input_ +b_;
output_ = getAct(sigma);
return output_;
}feedForward 라는 함수는 입력에 값이 들어오면 sigma 값을 계산하고 활성화 함수를 이용해서 바로 y값을 린턴하는 함수이다.
double Neuron::getActGrad(const double& x)
{
// linear or idenity activation fucntion
return 1.0;
}
getActGrad 는 getAct라는 함수의 미분값을 반환하는 함수이다.
여기선 1을 반환한다.

노란색 과정이다. f(sigma)= sigma 인데 일차적인 관계 이므로 이값은 1
void Neuron::propBacward(const double& target)
{
const double alpha = 0.1; // lerning rate
const double grad = (output_ - target) * getActGrad(output_);
w_ -= alpha * grad * input_; // last input_) came from d(wx+b)/dw =x
b_ -= alpha * grad * 1.0; // last 1.0 came from d(wx+b)/db = 1
}
propBacward 역전파 과정이다. 내가 목표로 하는 타겟을 찾는 과정에서 w값과 b값을 조정한다.
여기서 알파는 0.1로 고정 했다.

위쪽에 설명한 식을 구하기 위해서 라운드E/라운드Y값을 알수있다.
(output_ - target)이 되고 라운드Y/라운드F 값은 1인것은 생각해보면 알수있다.
(출력값 자체가 어떤 함수 f라는 것의 통과해야만 나오는 결과이므로 1:1관계임)
getActGrad는 라운드f/라운드 sigma 값이다.

이값은 input_값으로 할수있다. 왜냐 sigma 는 (wx+b) 값인데 x는 입력값이다. 미분해보면 input값만남는다.
b_의 경우에는 미분하면 1이기에 1.0을 곱한다.
int main()
{
Neuron My_neuron(2.0,1.0);
for(int i=0;i<100;i++)
{
cout<<"Trainin "<<i<<endl;
My_neuron.feedForward(1.0);
My_neuron.propBacward(4.0);
cout<<"w = "<<My_neuron.w_ << " b = "<<My_neuron.b_<<endl;
}
return 0;
}
메인문이다 인풋 1을 주엇을때 아웃풋 4가 되렬면 w와 b가 얼마가 되야하는가를 프로그램에게 묻고있다.
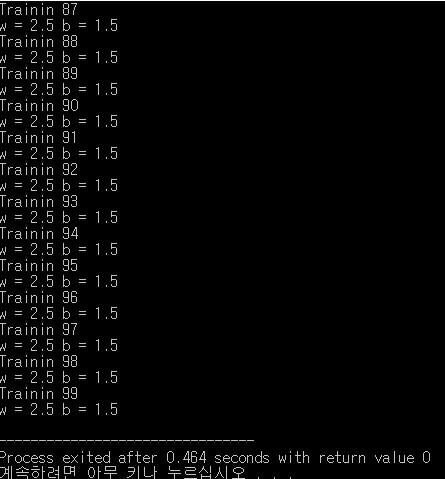
원하는 값이 구해지는걸 알수있다. 딥러닝의 역전파를 이용해서 원하는 값에 도달하는 방법을 알아보았다
전체소스
#include <iostream>
using namespace std;
class Neuron
{
public:
double w_;
double b_;
double input_;
double output_; // saved for back-prop
Neuron();
Neuron(const double& w_input,const double& b_input);
double getAct(const double& x);
double feedForward(const double& _input);
double getActGrad(const double& x);
void propBacward(const double& target);
};
Neuron::Neuron()
{
w_=2.0;
b_=1.0;
}
Neuron::Neuron(const double& w_input,const double& b_input)
{
this->w_ = w_input;
this->b_ = b_input;
}
double Neuron::getAct(const double& x) // 함수과정
{
return x;
}
double Neuron::feedForward(const double& _input) // 시그마와 함수 과정
{
input_ = _input;
const double sigma = w_ * input_ +b_;
output_ = getAct(sigma);
return output_;
}
double Neuron::getActGrad(const double& x)//미
{
// linear or idenity activation fucntion
return 1.0;
}
void Neuron::propBacward(const double& target)
{
const double alpha = 0.1; // lerning rate
const double grad = (output_ - target) * getActGrad(output_);
w_ -= alpha * grad * input_; // last input_) came from d(wx+b)/dw =x
b_ -= alpha * grad * 1.0; // last 1.0 came from d(wx+b)/db = 1
}
int main()
{
Neuron My_neuron(2.0,1.0);
for(int i=0;i<100;i++)
{
cout<<"Trainin "<<i<<endl;
My_neuron.feedForward(1.0);
My_neuron.propBacward(4.0);
cout<<"w = "<<My_neuron.w_ << " b = "<<My_neuron.b_<<endl;
}
return 0;
}
'개인공부' 카테고리의 다른 글
| tensorflow를 이용해서 binary 값 데이터 학습하기 (0) | 2020.07.04 |
|---|---|
| python::tensorflow (0) | 2020.07.04 |
| C++::Artificial Neural Network(인공신경망) (0) | 2020.07.04 |
| 안드로이드 : 계산기 어플 만들기 (0) | 2020.07.04 |
| 안드로이드 : 시작하기 (0) | 2020.07.04 |



