Tree? 트리 구조란 그래프의 일종으로, 여러 노드가 한 노드를 가리킬 수 없는 구조이다. 간단하게는 회로가 없고, 서로 다른 두 노드를 잇는 길이 하나뿐인 그래프를 트리라고 부른다
AVL Tree 란 만든사람의 본명을 한글자싞 합쳐서 나온 Tree이다.
이분 그래프에서 탐색을 할 때 시간복잡도는 트리의 높이(h) 에 따라 시간복잡도 O(h)를 가진다.

이런식의 한쪽으로 치우친 Tree를 어떻게 하면 효과적으로 Balacne Tree로 만들 수 있을 까?
이때 필요한 것이 AVL 트리이다.
좌 회전, 우 회전
LL Tree와 RR Tree를 소개하자면 LL은 말그대로 왼쪽으로 치우친 편향그래프이고 RR은 오른쪽으로 치우친 편향 그래프이다.


이 때 각 트리라는 것은 높이라는 값을 가지게되는데 Root 노드를 U라고 햇을 경우 왼쪽 서브트리의 높이와 오른쪽 서브트리의 높이 차이가 2이상 , 2이하일 경우 rotate를 진행 하게된다.

이런 식으로 편향 그래프 우측에 대해서 왼쪽 서브노드의 높이가 0 오른쪽 높이가 2 이므로 차이는 -2 가 되므로 좌 회전을 한다. 우회전도 마찬가지로 하면된다.
지금 까지의 회전을 싱글 로테이션이라고 하며 예시를 들어서 설명하겠다.
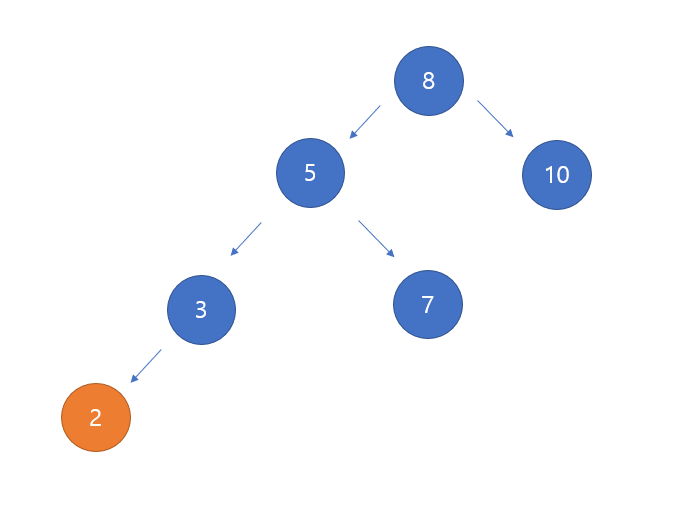
다음과 같이 기존 파란색 밸런스 트리에 2라는 값이 들어온 경우 root node를 기준으로 깊이의 차이가 2가 된다.
따라서 rrotate 가 필요하다. rrtoate에 따라 5가 root 노드가 될것이고 7은 8의 왼쪽 서브노드가 될것이다.

간다한 소스코드
fucntion lrotate(self):
# 현재 트리의 기존 root를 A라고 두자
A = self.node
# 기존 root의 right child를 B라고 두자
B = self.node.right.node
# B의 left child(위 그림에서 베타)를 T라고 두자
T = B.left.node
# B를 새로운 root로 지정
self.node = B
# A를 root(B)의 새로운 left child로 지정
B.left.node = A
# T(위 그림에서 베타)를 A의 새로운 right child로 지정
A.right.node = T쉽게 말해서 ^ 이런 Tree를 < 이런 Tree로 바꾸는게 left
fucntion rrotate(self):
A = self.node
B = self.node.left.node
T = B.right.node
self.node = B
B.right.node = A
A.left.node = T이것도 ^ 여기서 > 이렇게 바꾸는것을 right라고 한다.
하지만 한번의 회전만으로는 Balance Tree로 바꾸는 것은 어렵다.
두번 rotation 하는 경우

위와 같이 root 노드에서 왼쪽의 높이가 더높은 경우의 트리를 예로 들겠다. 한번의 회전으로는 균형 트리를 만들 수 없다. 이때는 두번을 회전을 하게된다.

먼저 주황색 노드를 기준으로 lroatae를 수행한다.

위와 같이 회전을 하게된다.
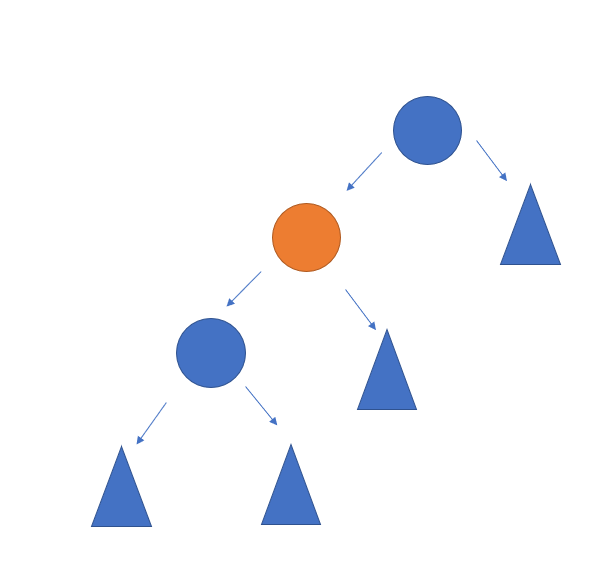
이제 다시 주황색을 중심으로 rroate를 하자.

밸런스트리가 만들어지는 것을 확인 할 수 있다.
'개인공부' 카테고리의 다른 글
| Quick Sort (0) | 2020.06.24 |
|---|---|
| B-Tree (0) | 2020.06.24 |
| Page Size (0) | 2020.06.23 |
| Replacement Strategies (0) | 2020.06.23 |
| Virtual Memory Management (0) | 2020.06.23 |

