트라이 알고리즘
일반 적인 정수들은 O(1) 시간내에 비교가 가능합니다 . 1==1 ,123>4 처럼 단순연산으로 접근 할 수 있습니다.
하지만 String 같은경우에는 "ABC" == "ABCD" 를 고려하기 위해서는 최대 문자열의 길이 O(M) 시간이 걸립니다.
(첫 번째 인덱스부터 계속 비교해 나가야 되기 때문입니다.)
따라서 기존 이진 트리로 정수형 데이터를 찾는데 걸리는 시간이 O(logN) 이라고한다면 문자열의 경우에는 O(MlongN) 시간이 걸리게 됩니다.
하지만 트라이 알고리즘을 사용한다면 O(M) 시간내에 자료를 찾을 수 가 있습니다.
문자열 집합 S={"BE","BET","BUS","TEA","TEN"} 을 트라이 자료구조로 표현하면 다음과 같습니다.
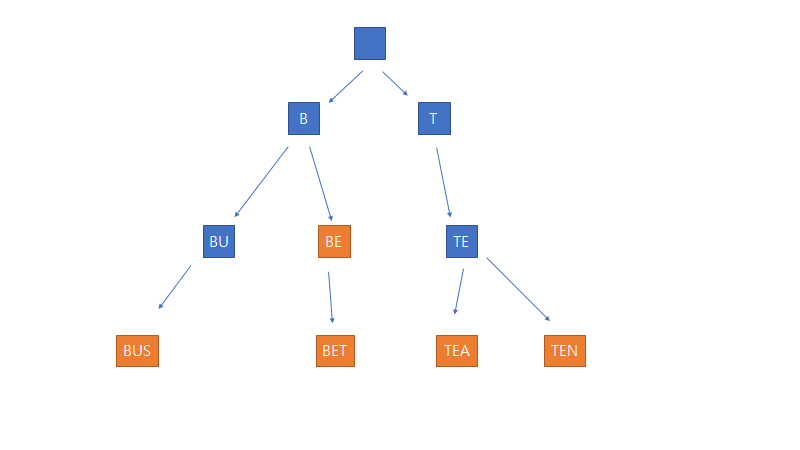
여기서 주황색으로 표시된 Node에 자료가 있다는 뜻으로 해석합니다. 이러한 자료구조를 하기위해서 다음과 같은 변수들이 필요합니다.
그림에서 볼 수 있듯이 트라이는 집합에 포함된 문자열의 접두사들에 대응되는 노드들이 서로 연결된 트리입니다.
한 접두사의 맨 뒤에 글자를 덧붙여 다른 접두사를 얻을 수 있을 때 두 노드는 부모 자시 관계로 연결됩니다. 두 노드를 연결하는 간선은 덧붙인 글자에 대응되는 것을 눈여겨봅시다. 트라이의 루트는 항상 길이 0인 문자열에 대응되며, 노드의 깊이가 깊어질 때마다 대응되는 문자열의 길이는 1씩 늘어납니다.
트라이는 노드는 대응되는 문자열을 저장할 필요가있습니다. 자손 노드들을 가리키는 포인터 목록과, 이 노드가 종료 노드인지를 나타내는 불린 값 변수로 구성됩니다.
단점 : 메모리가 많이 낭비된다.
장점 : 다음 노드를 찾는 과정에서 어떤 탐색도 필요하지 않는다.
구현 함수
문자의 개수 ALPHABET
문자를 숫자로 변환해주는 toNumbuer()
트라이에 문자를 추가 insert()
문자 찾는 find()
package 개인공부;
import java.util.Arrays;
import 개인공부.트라이.TrieNode;
public class 트라이 {
// 알파벳 사이즈
static final int ALPHABET = 26;
// 트라이 노드
static class TrieNode {
TrieNode[] children = new TrieNode[ALPHABET];
// isEndOfWord 가 true면은 실제 존재하는 노드다.
// end of a word
boolean isEndOfWord;
public TrieNode() {
isEndOfWord = false;
for (int i = 0; i < ALPHABET; ++i)
children[i] = null;
}
}
static TrieNode root;
static void insert(String key) {
int level;
int length = key.length();
int index;
TrieNode pCrawl = root;
for (level = 0; level < length; ++level) {
index = key.charAt(level) - 'a';
if (pCrawl.children[index] == null)
pCrawl.children[index] = new TrieNode();
pCrawl = pCrawl.children[index];
}
// for이 다놀고나면 가장 끝에 노드까지 다만들어진다.
// pCrawl 은 end 노드를 가리킬네니 true값으로 바꿔준다.
pCrawl.isEndOfWord = true;
}
static boolean search(String key) {
int level;
int length = key.length();
int index;
TrieNode pCrawl = root;
for (level = 0; level < length; ++level) {
index = key.charAt(level) - 'a';
if (pCrawl.children[index] == null)
return false;
pCrawl = pCrawl.children[index];
}
return (pCrawl != null && pCrawl.isEndOfWord);
}
}
각각의 클래스와 함수에 대해서 설명하자면
TrieNode Class
- children 자식 노드를 가진다 이때 하나의 노드는 알파벳의 수만큼 가질수 있다.
- isEndOfWord -> 현재노드가 끝으로 단어가 끝나는지 check한다.
- 생성자 Node를 생설할때 children[ALPHABET]은 null 값으로 초기화해준다.
static TriNode root 는 최상단의 노드이다 모든 노드들의 시작점
insert 함수
- key 현재 추가할 단어를 의미한다.
- level 은 key값의 단어하나하나를 접근할때 사용된다.
- index 는 알파벳 - > 숫자 로 바꾸어 배열에 접근 할 수 있게 해준다.
- pCrawl 는 root부터 시작해 포인터처럼 접근할때 사용된다.
insert를 하면서 자식노드가 null 이라면 생성해준다. 그리고 key값에 다음 문자가 존재한다면 pCrawl을 생성하거나 가리키는 chldren에 접근한다음 또 조사한다.
그렇게 조사가 끝나고나면 현재 pCrawl는 문자의 끝값을 가리키는 Node가되는데 isEndOfWord = true로 바꿔준다.
search도 insert와 같은 원리다.
index로 한 chldren의 node가 존재하지않는다는거는 Tree에 저장되지 않은 데이터라는 거니 false 반환
끝 단어까지 가진다면 그값이 만약 null값이 아니고 isEndOfword라면 존재하는 데이터다.
관련 문제로는 백준의 전화번호 목록이 있다.
https://www.acmicpc.net/problem/5052
5052번: 전화번호 목록
문제 전화번호 목록이 주어진다. 이때, 이 목록이 일관성이 있는지 없는지를 구하는 프로그램을 작성하시오. 전화번호 목록이 일관성을 유지하려면, 한 번호가 다른 번호의 접두어인 경우가 없어야 한다. 예를 들어, 전화번호 목록이 아래와 같은 경우를 생각해보자 긴급전화: 911 상근: 97 625 999 선영: 91 12 54 26 이 경우에 선영이에게 전화를 걸 수 있는 방법이 없다. 전화기를 들고 선영이 번호의 처음 세 자리를 누르는 순간 바로 긴급전화가
www.acmicpc.net
소스코드
package algo;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import algo.B5052.Trie;
public class B5052 {
static int T;
static int N;
static final int NUMS = 10;
static class Trie {
boolean isEndWord;
Trie children[];
public Trie() {
isEndWord = false;
children = new Trie[NUMS];
for (int i = 0; i < NUMS; ++i)
children[i] = null;
}
}
static Trie root;
static void insert(String key) {
Trie curTrie = root;
int length = key.length();
int level;
int index;
for (level = 0; level < length; ++level) {
index = key.charAt(level) - '0';
if (curTrie.children[index] == null) {
curTrie.children[index] = new Trie();
}
curTrie = curTrie.children[index];
}
curTrie.isEndWord = true;
}
static boolean available(String key) {
Trie curTrie = root;
int length = key.length();
int level;
int index;
for (level = 0; level < length; ++level) {
index = key.charAt(level) - '0';
if (curTrie.isEndWord)
return false;
curTrie = curTrie.children[index];
}
return true;
}
public static void main(String[] args) throws NumberFormatException, IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
T = Integer.parseInt(br.readLine());
for (int t = 1; t <= T; t++) {
N = Integer.parseInt(br.readLine());
root = new Trie();
String[] str = new String[N];
for (int n = 0; n < N; n++) {
str[n] = br.readLine();
insert(str[n]);
}
boolean ans = true;
for (int n = 0; n < N; n++) {
if (!available(str[n])) {
ans = false;
break;
}
}
if(ans)
sb.append("YES\n");
else
sb.append("NO\n");
}
System.out.print(sb.toString());
}
}'Algorithm' 카테고리의 다른 글
| CCW (0) | 2020.05.03 |
|---|---|
| 강한 연결 요소 java (0) | 2020.04.29 |
| 이분 매칭 알고리즘 ( JAVA),열혈강호1,2,3 문제 (0) | 2020.04.25 |
| 포드-폴커슨 인접리스트 구현하기 JAVA (0) | 2020.04.19 |
| 네트워크 유량 ( network flow) / 포드 - 풀커슨 알고리즘 JAVA (2) | 2020.04.19 |