반응형
Tree는 deep를 가지는 자료구조이다.
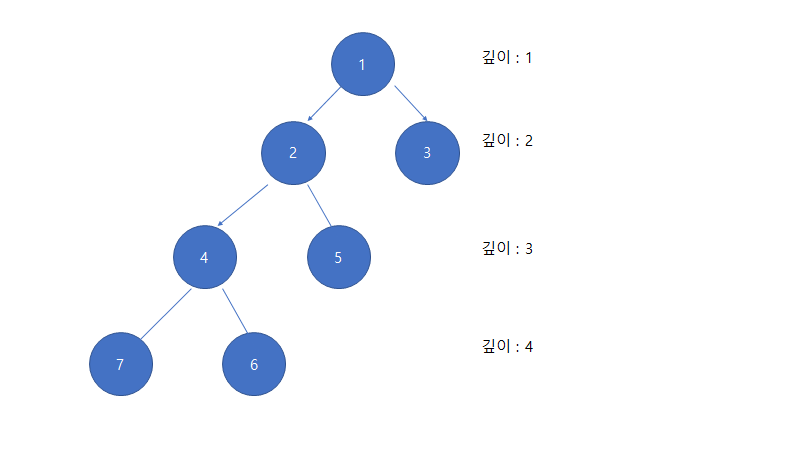
LCA는 직역하면 최소 공통 조상이라고 한다.

7과 5의 최소 공통 조상은 2 가될것이다. 문제를 푸는 방법은 7과 5의 deep중 깊은 deep를 위로 올리면서
같은 deep일때 써로를 비교해주는 O(N) 시간으로 문제를 해결 할수 있다.
하지만 만약 쿼리가 많은 문제에 대해서는 어떻게해야할까??
같은 깊이를 빠르게 찾을 특별한 자료구조가 필요해보인다.
7번을 보도록 하겠다.
7번의 1번째 조상은 4 2 번째 조상은 2 이다.
이러한값을 배열에 미리 저장해둔다면 공통 조상을 찾는데 걸리는 시간은 O(longN)이 된다. 처음 배열을 만드는 비용
O(N*K) 가드는데 K는 log2 ( 최대N) 을 해서 나올수 있는 값이다. N가 100000이라면 2^20 > N 이기때문에
K = 20의 시간복잡도를 가진다.
|
1
2
3
4
5
6
7
8
9
10
11
12
|
public static void Init(int n, int deep) {
deeps[n] = deep;
for (int next : ver[n]) {
if (deeps[next] != 0)
continue;
// parrent 를 초기화 시킨다.
parrent[next][0] = n;
Init(next, deep + 1);
}
}
http://colorscripter.com/info#e" target="_blank" style="color:#4f4f4ftext-decoration:none">Colored by Color Scripter
|
n : 현재노드 deep : 깊이
DFS 탐색을 통해서 트리자료구조를 1번에서 출발하면서 깊이를 저장한다.
parrent는 2^0 번째 2^1번째 2^2.... 2^20 번째 부모가 누군지 저장하는 배열이다.
2^0번째 배열은 DFS를 들어가기전 노드가 되므로 parrent[next][0] = n 이된다.
|
1
2
3
4
5
6
7
8
|
public static void Initf() {
for(int j=1;j<=20;j++) {
for(int n=1;n<=N;n++) {
parrent[n][j] = parrent[parrent[n][j-1]][j-1];
}
}
}
http://colorscripter.com/info#e" target="_blank" style="color:#4f4f4ftext-decoration:none">Colored by Color Scripter
|
2^0 번째 조상은 Init을 처리할때 함께 처리해줫다. 이제는 2^1번째 2^2 번째의 조상을 찾아야한다.
어떤 노드의 2^1번째조상은 노드의 2^0번째 조상의 2^0번째 조상인것을 알수가있다.
어떤노드 2^8번째 조상은 노드의 2^7번째 조상의 2^번째 조상이다.
2^ 8 = 2^7 + 2^7 이기때문이다.
그걸 코드로 표현한다면 parrent[n][j] = parrent[parrent[n][j-1]][j-1] 가 된다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
public static int Solve(int x, int y) {
if(deeps[x] > deeps[y]) {
int tmp = x;
x = y;
y = tmp;
}
// deeps[x] <= deeps[y] 상태
for(int j=20;j>=0;j--) {
if(deeps[y]-deeps[x] >= (1<<j)) {
y = parrent[y][j];
}
}
if(y==x) return y;
for(int j=20;j>=0;j--) {
if(parrent[x][j]!=parrent[y][j]) {
x = parrent[x][j];
y = parrent[y][j];
}
}
return parrent[x][0];
}
http://colorscripter.com/info#e" target="_blank" style="color:#4f4f4ftext-decoration:none">Colored by Color Scripter
|
모든노드들의 조상에 대한 조사가 다끝낫으면 이제 우리는 빠르게 조상이 누구인지 찾을수가 있다.
먼저 두노드 x, y에대해서 deeps를 조사한다 .만약 서로 deeps가 다르다면 같은 deeps까지 만들어준다.
2^j 형식 deeps가 커지므로 두 x y 의 deeps 으 차이만큼으로 접근한다.
그렇게 같은 deeps가되엇을때 x y 값이 같다면 정답이고 다르다면 x y deeps를 j=20 부터 맞추어나간다.
만약 서로 deeps에서 조상이 같다면 처음으로 다른 조상이 나오는 j값을 찾는다.
그럼 x y 를 그조상으로 이동시킨다.
어떤수를 찾아갈때는 2^a + 2^b + 2^c ( a>b+c) 형태로 표현이 가능하기때문에 for문으로 저렇게 표현한다.
11438번: LCA 2
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정점 쌍이 주어진다.
www.acmicpc.net
전체소스
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
|
package day0330;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
public class B11438 {
static int N, M;
static ArrayList<Integer> ver[];
static int parrent[][];
static int deeps[];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String str[];
N = Integer.parseInt(br.readLine());
ver = new ArrayList[N + 1];
for (int n = 1; n <= N; n++) {
ver[n] = new ArrayList<Integer>();
}
for (int i = 0; i < N - 1; i++) {
str = br.readLine().split(" ");
int u = Integer.parseInt(str[0]);
int v = Integer.parseInt(str[1]);
ver[u].add(v);
ver[v].add(u);
}
// 2^i 번째 부모 최신화 하기
parrent = new int[100001][21];
deeps = new int[100001];
Init(1, 1);
Initf();
M = Integer.parseInt(br.readLine());
StringBuilder sb = new StringBuilder();
for (int i = 0; i < M; i++) {
str = br.readLine().split(" ");
}
System.out.print(sb.toString());
}
public static void Initf() {
for(int j=1;j<=20;j++) {
for(int n=1;n<=N;n++) {
parrent[n][j] = parrent[parrent[n][j-1]][j-1];
}
}
}
public static void Init(int n, int deep) {
deeps[n] = deep;
for (int next : ver[n]) {
if (deeps[next] != 0)
continue;
// parrent 를 초기화 시킨다.
parrent[next][0] = n;
Init(next, deep + 1);
}
}
public static int Solve(int x, int y) {
if(deeps[x] > deeps[y]) {
int tmp = x;
x = y;
y = tmp;
}
// deeps[x] <= deeps[y] 상태
for(int j=20;j>=0;j--) {
if(deeps[y]-deeps[x] >= (1<<j)) {
y = parrent[y][j];
}
}
if(y==x) return y;
for(int j=20;j>=0;j--) {
if(parrent[x][j]!=parrent[y][j]) {
x = parrent[x][j];
y = parrent[y][j];
}
}
return parrent[x][0];
}
}
http://colorscripter.com/info#e" target="_blank" style="color:#4f4f4ftext-decoration:none">Colored by Color Scripter
|
반응형
'Algorithm' 카테고리의 다른 글
| 투 포인터 알고리즘 (0) | 2020.04.06 |
|---|---|
| 알고리즘 공부할것들 (0) | 2020.04.02 |
| LinkedList : java (0) | 2020.03.18 |
| 파라메트릭 (0) | 2020.03.13 |
| JAVA : nextPermutation 다음순열 (2) | 2020.03.12 |
